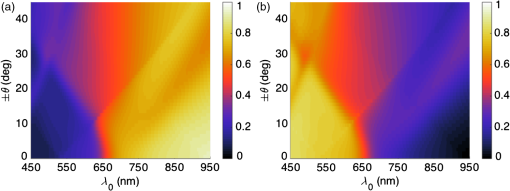
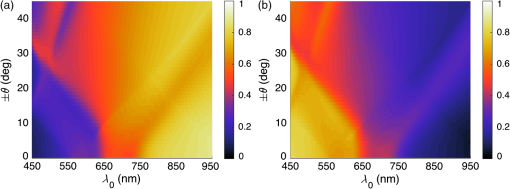
1.

Introduction

The efficiency of a solar cell varies with the (free-space) wavelength. Some semiconductors are more efficient harvesters of solar energy at longer wavelengths, others at shorter wavelengths.¹ If the incident solar light could be split such that light below a cutoff wavelength is directed to a solar cell that is efficient in that spectral regime, while light at wavelengths above the cutoff wavelength is directed to another solar cell that is efficient in that spectral regime, then maximal harvesting of solar energy could become possible. So a spectrum splitter could be used to spatially multiplex different solar cells that have high efficiency in mutually exclusive parts of the solar spectrum. This fundamental concept, proposed in 1955 (Ref. 1), is still a hot topic for research.^2–6

Recent experimental work has focused on the spectrum-splitting concept using a hybrid arrangement of silicon and dye-sensitized solar cells.⁵ In these experiments, a bandstop filter on the entry pupil of a dye-sensitized solar cell was used to reflect and concentrate near-infrared light onto a silicon p-n junction cell. As an alternative to that approach, we theoretically examined the use of a grating made of dielectric materials for specularly transmitting light of longer wavelengths while light of shorter wavelengths predominately transmitted nonspecularly. Such a grating could be placed on top of a lens to selectively focus and concentrate long-wavelength light onto a silicon absorber while deflecting short-wavelength visible light to the back plane of a large-area absorber, such as a dye-sensitized solar cell.

An obvious question arises: how to optimize the geometry and material constituents of a spectrum splitter in order to obtain the best performance. In this paper, we show that a combination of the rigorous coupled-wave approach (RCWA) to determine the reflection and transmission characteristics of the grating^7,8 with the differential evolution algorithm (DEA) for optimizing the geometry and the refractive indices of the material constituents^9–12 gives a useful design tool.

Our approach to splitter design is to apply optimization to improve a basic design that already shows promise of spectrum splitting. We examined the two candidate splitters shown in Fig. 1. For both candidates, the grating lines were taken to be infinitely long and parallel to the $y$ axis in a Cartesian coordinate system, the grating was assumed to be of infinite extent along the $x$ axis with period $L$, the height of the host dielectric slab was set equal to $d$, the half space $z<0$ was taken to be occupied by air with refractive index $n_a=1$, and the half space $z>d$ was taken to be occupied by glass with refractive index $n_g$. Light was taken to be incident on either splitter from the half space $z<0$, the wave vector of the incident light lying wholly in the $xz$ plane and oriented at an angle $\theta$ with respect to the $z$ axis, where $\theta$ is taken to be positive when measured counterclockwise and negative when measured clockwise.

Fig. 1

Two candidate structures for splitting the solar spectrum: (a) the candidate splitter that is predicted to work well but will pose manufacturing challenges and (b) the candidate splitter that is predicted to be sensitive to the angle of incidence of light with respect to the $z$ axis but would be easier to manufacture than the other candidate.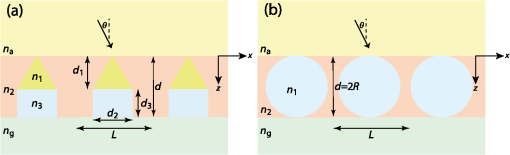

The free parameters for the splitter containing the triangle-topped rectangular grating elements in Fig. 1(a) were taken as $L$, $d_1$, $d_2$, $d_3=d-d_1$, $n_1$, and $n_2$, but $n_3$ was assumed to be fixed. The free parameters for the splitter containing the circular grating elements of radius $R$ in Fig. 1(b) were taken as $L$, $R=d/2$, $n_1$, and $n_2$. Useful improvements to the basic design were obtained. Application of the DEA indicated that significant spectrum splitting can be achieved if the angle of incidence $\theta \in [-15\mathrm{deg},15\mathrm{deg}]$.

The paper proceeds as follows. In Sec. 2, we briefly outline the RCWA used to predict the transmission and reflection coefficients of a grating. The DEA for optimization is described in Sec. 3. For both candidate splitters, numerical results are provided in Sec. 4, allowing us to predict the degree of spectrum splitting. Concluding remarks are presented in Sec. 5.

Vectors are denoted in boldface. The Cartesian unit vectors are denoted as ${\widehat{\mathbf{u}}}_x$, ${\widehat{\mathbf{u}}}_y$, and ${\widehat{\mathbf{u}}}_z$. During the application of CWA, an $\exp (-i\omega t)$ dependence on time $t$ was assumed for all electric and magnetic field phasors with $i=\sqrt{-1}$ and $\omega$ as the angular frequency. Furthermore, the free-space wavenumber is denoted by $k_0=\omega \sqrt{{\epsilon }_0{\mu }_0}$ and the free-space wavelength by ${\lambda }_0=2\pi /k_0$, with ${\epsilon }_0$ as the permittivity and ${\mu }_0$ as the permeability of free space.

2.

Rigorous Coupled-Wave Approach

In the half space $z<0$, incident sunlight is modeled as a spectrum of plane waves propagating in the $xz$ plane at an angle $\theta$ with respect to the $z$ axis. A plane wave can be either $p$ polarized or $s$ polarized. As depolarization cannot be caused by the splitter, the two polarization states can be tackled separately.

3.

Differential Evolution Algorithm

We implemented the DEA (Refs. 9 and 10) to seek an optimal design for each of the two candidate splitters shown in Fig. 1. The DEA is a genetic algorithm that iteratively improves a candidate solution with regard to a given measure of quality, given an initial guess in the search space together with several other candidate solutions. The algorithm attempts to avoid local minimums by stochastic choices of the updates at each step. A large space of candidate solutions can be searched, but a global minimum is not guaranteed. It is helpful to limit the search space and have a good initial choice of the free parameters. Therefore, we used this algorithm in conjunction with the conclusions gleaned from inspection of RCWA results for both candidate splitters.^11,12

In brief, let $v=(v_1,v_2,v_3,\dots ,v_{\tilde{n}})$ denote a point in the search space $\mathcal{S}\subset {\mathbb{R}}^{\tilde{n}}$ for the free parameters that can be varied to obtain an optimal design, $\tilde{n}$ being the number of components of $v$. The objective is to find $v^{\text{opt}}$ that minimizes a given cost functional $\mathsf{F}:\mathcal{S}\subset {\mathbb{R}}^{\tilde{n}}\to \mathbb{R}$. Besides the cost functional $\mathsf{F}$ and the search space $\mathcal{S}$, the algorithm requires the choice of three parameters. First, the number $M$ of candidate points in $\mathcal{S}$ has to be chosen. These candidate points constitute the population of solutions. Next, a differential weight $\alpha \in (\mathrm{0,2})$ must be chosen to govern the mutation of three distinct points in $\mathcal{S}$ to obtain a new donor point. Finally, a crossover probability $C\in (\mathrm{0,1})$ is prescribed to select entries in a donor point to construct a new candidate point for a better solution in a process called recombination. Once the new candidate point is formed, the value of $\mathsf{F}$ at this point is compared to the value at the current point, and the new point is used if it improves the functional’s value. Details of the algorithm itself are described in a preceding paper.¹¹

Let us note that $\tilde{n}=6$ and $v=(L,d_1,d_2,d_3,n_1,n_2)$ for the splitter with triangle-topped rectangular grating elements, whereas $\tilde{n}=4$ and $v=(L,R,n_1,n_2)$ for the splitter with circular grating elements.

4.

Numerical Results and Discussion

An optimal splitter would transmit 100% of the energy to specular modes above a specified cutoff wavelength ${\lambda }_c$, and 100% of the energy to nonspecular modes for wavelengths below ${\lambda }_c$. Obviously, an ideal splitter cannot be obtained in practice. Therefore, our objective was to optimize the geometry of the two splitters shown in Fig. 1 such that (1) as much light as possible is transmitted as nonspecular Floquet harmonics for ${\lambda }_0<{\lambda }_c$ and (2) as much light as possible is transmitted as the specular Floquet harmonic for ${\lambda }_0>{\lambda }_c$. Since the nonspecular Floquet harmonics transport energy in directions different from the specular direction, different energy-harvesting devices can be used for the two spectral regimes.

Accordingly, we set the cost functional

For all results presented here, we used horizontal layers of thickness 5 nm for the piecewise-uniform approximation of the coefficients ${\upsilon }_r^{(n)}(z,{\lambda }_0)$ and ${\epsilon }_r^{(n)}(z,{\lambda }_0)$ for $z\in (0,d)$, and we fixed $N_t=14$ after ensuring that the principle of conservation of energy¹³ was satisfied with an error <0.01%. Furthermore, we selected $M=10\tilde{n}$, $\alpha =0.8$, and $C=0.7$ for the DEA.

Although good separation of specular and nonspecular transmissions for a wide range of angles of incidence is highly desirable, the process of averaging $\mathsf{F}$ over $\theta$—in addition to averaging over ${\lambda }_0$—would greatly increase computational time. So we started by fixing $\theta =6\mathrm{deg}$ for optimization, but then explored how the optimal splitters would perform at other angles of incidence. Let us note that $T^{(0)}$, $T^{n\ne 0}$, $R^{(0)}$, and $R^{n\ne 0}$ do not depend on the sign of $\theta \in (-90\mathrm{deg},90\mathrm{deg})$, because the unit cells of both candidate splitters are symmetric about the $z$ axis.

For the numerical results presented in this paper, we chose SF11 glass as the material in the half space $z>d$ of transmission. The refractive index $n_g$ as a function of ${\lambda }_0$ is available in the literature.¹⁵ As mentioned in the previous section, we set $n_a=1$. Both of these choices are consistent with the use of spectrum splitters for solar cells. Fixing ${\lambda }_{0_{\text{min}}}=450\mathrm{nm}$ and ${\lambda }_{0_{\text{max}}}=950\mathrm{nm}$, we set the wavelength ${\lambda }_c=650\mathrm{nm}$ for the switch between specular and nonspecular scattering. We also assumed $n_{\mathrm{1,2},3}$ to be real and independent of ${\lambda }_0$, thereby confining the scope of our results to materials with weak dissipation and weak dispersion in the chosen spectral regime. All computational codes were written in MATLAB® and implemented on a LINUX machine Dell PowerEdge R620 configured with 15K SAS Drives and 320 GB of RAM. Version 2014a of 64-bit MATLAB® was used.

4.1.

Optimization of the Splitter with Triangle-Topped Rectangular Grating Elements

We began with the optimization of the splitter shown in Fig. 1(a). We set $n_3$ to be the ${\lambda }_0$-dependent refractive index of a specific composite material (glass: 47% titania and 53% silica) shown in Fig. 2. We set

Eq. (28)

$$L=500\mathrm{nm},d_1=100\mathrm{nm},d_2/L=0.5,d_3=100\mathrm{nm},n_1=1.6,n_2=1$$

as the initial guess for the DEA. As mentioned in Sec. 3, this initial guess for $v$ was used as one member of the $M$ candidate points in the DEA.

Fig. 2

Refractive index $n_3$ of the chosen composite material (containing 47% titania and 53% silica) as a function of 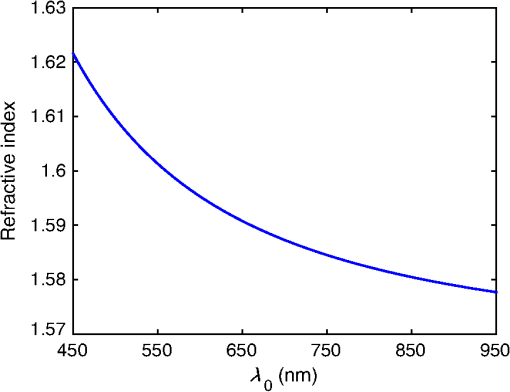${\lambda }_0$.

Figure 3 presents the spectrums of $T^{(0)}$, $T^{n\ne 0}$, $R^{(0)}$, and $R^{n\ne 0}$ for $\theta \in \{\pm 6\mathrm{deg},\pm 15\mathrm{deg}\}$ with the initial guess (28). At both angles of incidence, there is a tendency to shift between specular and nonspecular transmission as the wavelength changes, but the effect is not large.

Fig. 3

$T^{(0)}$, $T^{n\ne 0}$, $R^{(0)}$, and $R^{n\ne 0}$ as functions of ${\lambda }_0$ for the splitter with the triangle-topped rectangular grating elements described by the initial guess (28): (a) 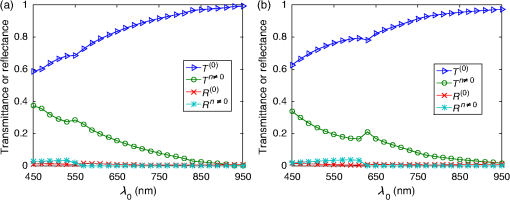$\theta =\pm 6\mathrm{deg}$ and (b) $\theta =\pm 15\mathrm{deg}$.

For optimization, the free parameters were constrained to lie in the following search space $\mathcal{S}$:

Eq. (29)

$$\begin{gathered} L\in [300,700]\mathrm{nm},d_1\in [50,300]\mathrm{nm},d_2/L\in [0.2,0.9], \\ {d}_3\in [50,300]\mathrm{nm},n_1\in [1,2.4],n_2\in [1,2.4]. \end{gathered}$$

As the DEA allows the user to set a minimum step size for updating each free parameter in the search space, we used the following minimum step sizes: 10 nm for $L$; 5 nm for $d_1$ and $d_3$; and 0.1 for $n_1$, $n_2$, and $d_2/L$.

After optimization for $\theta =6\mathrm{deg}$, we obtained the following parameters using 100 iterations of the DEA:

Eq. (30)

$$L=530\mathrm{nm},d_1=295\mathrm{nm},d_2/L=0.7,d_3=135\mathrm{nm},n_1=2.0,n_2=1.0.$$

The progress of the cost functional $\mathsf{F}$ toward the optimal design is shown in Fig. 4. The DEA reduced the value of $\mathsf{F}$ by $\sim 37.4\%$ within 50 iterations.

Fig. 4

Values of the cost functional $F$ during the first 50 iterations of the differential evolution algorithm (DEA) for the splitter with the triangle-topped rectangular grating elements. These calculations were done for 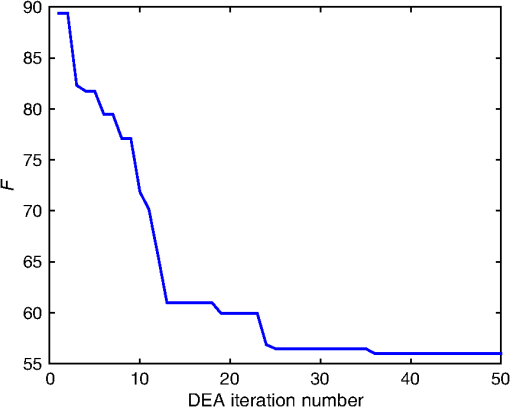$\theta =6\mathrm{deg}$.

Figure 5 presents the spectrums of $T^{(0)}$, $T^{n\ne 0}$, $R^{(0)}$, and $R^{n\ne 0}$ for $\theta \in \{\pm 6\mathrm{deg},\pm 15\mathrm{deg}\}$ with the optimal parameters (30). Clearly, the short-wavelength behavior is much improved in comparison to Fig. 3. Furthermore, there is a definite switch around ${\lambda }_c=650\mathrm{nm}$, as desired. The switch blue shifts at a more oblique incidence, per the right panel of Fig. 5.

Fig. 5

Same as Fig. 3, except using the optimal parameters (30): (a) $\theta =\pm 6\mathrm{deg}$ and (b) $\theta =\pm 15\mathrm{deg}$. Optimization was performed for $\theta =6\mathrm{deg}$ and the crossover of the specular and nonspecular transmittances occurs at ${\lambda }_0=650\mathrm{nm}$ as desired. The crossover point blue shifts for 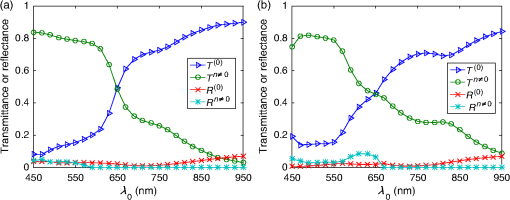$\theta =15\mathrm{deg}$.

In order to present a complete picture of the behavior of the splitter after optimization, in Fig. 6 we present density plots of $T^{(0)}$ and $T^{n\ne 0}$ as functions of $\theta$ and ${\lambda }_0$. Ideally, the left panel of Fig. 6 would be dark to the left of ${\lambda }_0={\lambda }_c$, while the right panel would reverse this. Provided that the incidence is not very oblique (say, $|\theta |<15\mathrm{deg}$), there is an obvious switch in energy between the specular and nonspecular modes of transmission, but this switch occurs at somewhat shorter wavelengths as the angle of incidence shifts from 0 deg.

Fig. 6

Density plots of (a) $T^{(0)}$ and (b) $T^{n\ne 0}$ against $\theta \in [-45\mathrm{deg},45\mathrm{deg}]$ and ${\lambda }_0\in [\mathrm{450,950}]\mathrm{nm}$ for the splitter with the triangle-topped rectangular grating elements described by the optimal parameters (30).

4.2.

Optimization of the Splitter with Circular Grating Elements

As the splitter with the triangle-topped rectangular grating elements considered in Sec. 4.1 would be difficult to manufacture, we turned our attention to the splitter with circular grating elements shown in Fig. 1(b). The following search space $\mathcal{S}$ was fixed:

Eq. (31)

$$L\in [300,600]\mathrm{nm},R/L\in [0.1,0.5],n_1\in [1,2],n_2\in [1,\sqrt{2}].$$

We used the following minimum step sizes: 10 nm for $L$, 0.01 for $R/L$, and 0.1 for $n_1$ and $n_2$.

The initial guess for the DEA was chosen as follows:

Eq. (32)

$$L=600\mathrm{nm},R/L=0.25,n_1=1.5,n_2=1.$$

With these parameters, the reflection and transmission characteristics of the splitter before optimization are shown in Fig. 7. While a tendency toward spectrum splitting is evident, the splitter does not perform well in the short-wavelength regime.

Fig. 7

$T^{(0)}$, $T^{n\ne 0}$, $R^{(0)}$, and $R^{n\ne 0}$ as functions of ${\lambda }_0$ for the splitter with the circular grating elements described by the initial guess (32): (a) 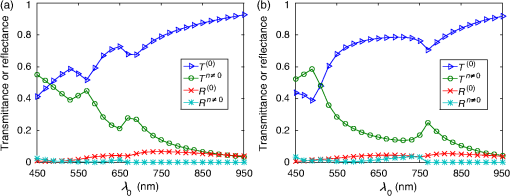$\theta =\pm 6\mathrm{deg}$ and (b) $\theta =\pm 15\mathrm{deg}$.

4.2.1.

Optimization at $\theta =\mathsf{6}\mathsf{deg}$

Application of the DEA (with $\theta =6\mathrm{deg}$ fixed) provided definite improvement. The progress of the optimization scheme is shown in Fig. 8. The cost functional $\mathsf{F}$ decreased by $\sim 68\%$ in the first 10 iterations (with the first iteration alone accounting for $\sim 46\%$) and stayed flat thereafter. The parameters $L$, $R/L$, $n_1$, and $n_2$ showed similar trends as the DEA progressed, as shown in Fig. 9.

Fig. 8

Values of the cost functional $\mathsf{F}$ during the first 50 iterations of the DEA for the splitter with the circular grating elements. These calculations were done for 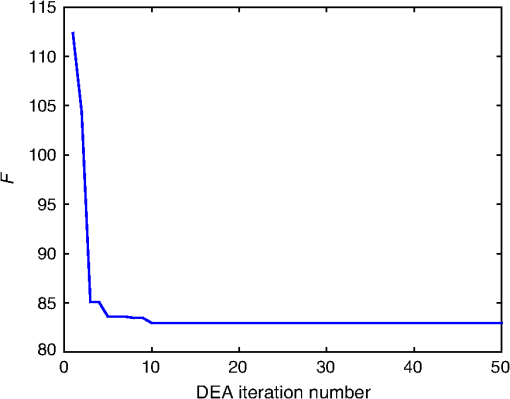$\theta =6\mathrm{deg}$.

Fig. 9

Parameters $L$, $R/L$, $n_1$, and $n_2$ during the first 50 iterations of the DEA for the splitter with the circular grating elements. These calculations were done for $\theta =6\mathrm{deg}$. The initial guesses are not shown.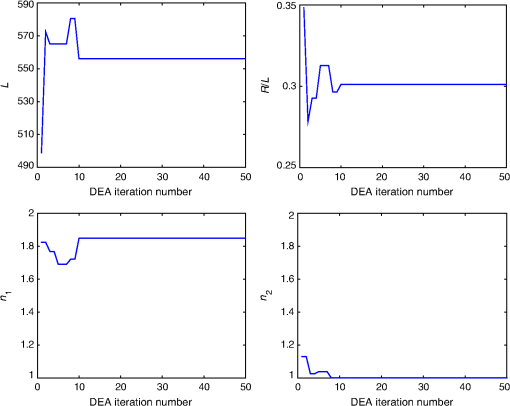

After 100 iterations of the DEA, we obtained the following optimal parameters:

Eq. (33)

$$L=560\mathrm{nm},R/L=0.3,n_1=1.8,n_2=1.0.$$

With these parameters, the reflection and transmission characteristics of the device are shown in Fig. 10. Despite the relatively small decrease in the cost functional during optimization, the left panel of Fig. 10 ($\theta =\pm 6\mathrm{deg}$) shows markedly improved short-wavelength behavior with an obvious splitting around ${\lambda }_c=650\mathrm{nm}$.

Fig. 10

Same as Fig. 7, except using the optimal parameters (33): (a) $\theta =\pm 6\mathrm{deg}$ and (b) $\theta =\pm 15\mathrm{deg}$. Optimization was performed for $\theta =6\mathrm{deg}$ and the crossover of the specular and nonspecular transmittances occurs at ${\lambda }_0=650\mathrm{nm}$ as desired. The crossover point blue shifts for 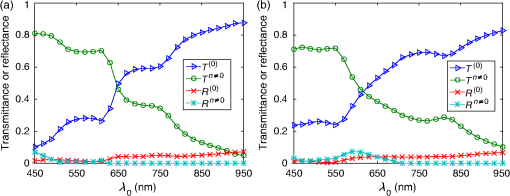$\theta =15\mathrm{deg}$.

In order to further illustrate the dependence of the splitter’s performance on the angle of incidence $\theta$, in Fig. 11 we present density plots of $T^{(0)}$ and $T^{n\ne 0}$ as functions of $\theta$ and ${\lambda }_0$. In comparison to the splitter with triangle-topped rectangular grating elements (Fig. 6), the splitter with circular grating elements shows a poorer performance for more oblique incidence.

Fig. 11

Density plots of (a) $T^{(0)}$ and (b) $T^{n\ne 0}$ against $\theta \in [-45\mathrm{deg},45\mathrm{deg}]$ and ${\lambda }_0\in [\mathrm{450,950}]\mathrm{nm}$ described by the optimal parameters (33).

4.2.2.

Optimization at $\mathsf{\theta }=\mathsf{15}\mathsf{deg}$

Next, we chose to optimize at $\theta =15\mathrm{deg}$ in order to try to improve the performance of the device away from normal incidence. Through trial and error in search of a better result than in Sec. 4.2.1, we also enlarged the search space $\mathcal{S}$ as follows:

Eq. (34)

$$L\in [300,600]\mathrm{nm},R/L\in [0.1,0.5],n_1\in [1.0,2.6],n_2\in [1.0,2.6].$$

However, we still used the initial guess (32).

After 100 iterations of the DEA (with $\theta =15\mathrm{deg}$ fixed), we obtained the following optimal parameters:

Eq. (35)

$$L=430\mathrm{nm},R/L=0.25,n_1=1.11,n_2=2.40.$$

The progress of the optimization scheme is shown in Fig. 12, the cost functional $\mathsf{F}$ decreasing by $\sim 30\%$ in the first 20 iterations and staying flat thereafter.

Fig. 12

Values of the cost functional $\mathsf{F}$ during the first 50 iterations of the DEA for the splitter with the circular grating elements. These calculations were done for 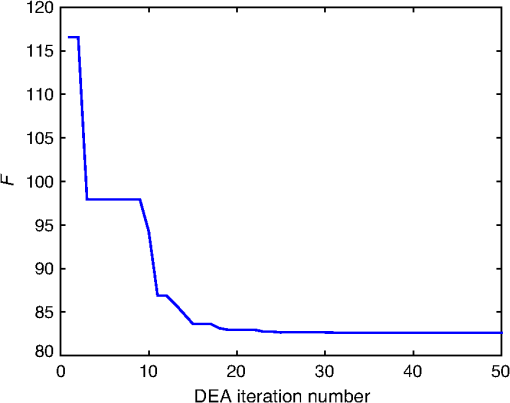$\theta =15\mathrm{deg}$.

The reflection and transmission characteristics of the optimal device are shown in Fig. 13. Even though the functional for optimization at $\theta =15\mathrm{deg}$ acquires the same value as for optimization at $\theta =6\mathrm{deg}$, as may be gleaned from comparing Figs. 8 and 12, the performance (Fig. 13) of the solution (35) is rougher than the performance (Fig. 10) of the solution (33). Nevertheless, the crossover at ${\lambda }_c=650\mathrm{nm}$ occurs at both values of $\theta$. However, note that the optimal choice involves $n_1>n_2$ for $\theta =6\mathrm{deg}$ in Sec. 4.2.1, but $n_1<n_2$ for the optimal choice for $\theta =15\mathrm{deg}$. This reversal needs to be explained and we do that in Sec. 4.2.3, as well as investigating further the shape of the cost functional $\mathsf{F}$ as a function of the free parameters.

Fig. 13

Same as Fig. 7, except using the optimal parameters (35): (a) $\theta =\pm 6\mathrm{deg}$ and (b) $\theta =\pm 15\mathrm{deg}$. Optimization was performed for $\theta =15\mathrm{deg}$ and the crossover of the specular and nonspecular transmittances occurs at ${\lambda }_0=650\mathrm{nm}$ as desired for both angles of incidence.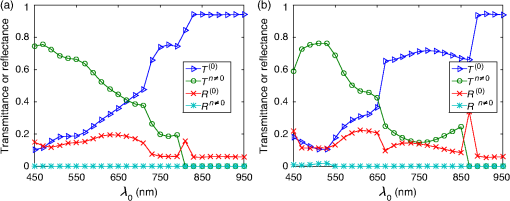

Density plots of $T^{(0)}$ and $T^{n\ne 0}$ as functions of $\theta$ and ${\lambda }_0$ are presented in Fig. 14. Again, in comparison to the splitter with triangle-topped rectangular grating elements (Fig. 6), the splitter with circular grating elements shows a poorer performance for more oblique incidence. In comparison to Fig. 11, the crossover in Fig. 14 at $\theta =12\mathrm{deg}$ is sharp and blueshifts steadily as the incidence becomes more oblique. The difference is due to optimizations performed for different values of $\theta$.

Fig. 14

Density plots of (a) $T^{(0)}$ and (b) $T^{n\ne 0}$ against $\theta \in [-45\mathrm{deg},45\mathrm{deg}]$ and ${\lambda }_0\in [\mathrm{450,950}]\mathrm{nm}$ for the splitter with the circular grating elements described by the optimal parameters (35). This figure should be compared to Fig. 11.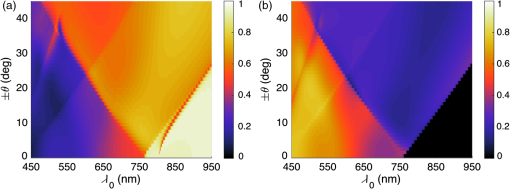

4.2.3.

Comparative analysis

The spectrums in Fig. 13 are more irregular than in Fig. 10 and are accompanied by a reversal of high refractive index and low refractive index regions. Thus, we investigated the functional $\mathsf{F}$ to help confirm that the optimum had indeed been reached.

First, we fixed $n_1=1.11$, $n_2=2.40$, and $R/L=0.25$ (i.e., at their optimal values), and then plotted $\mathsf{F}$ against $L$. Figure 15(a) shows that $\mathsf{F}$ as a function of $L$ has a single minimum—at $L=430\mathrm{nm}$, the value yielded by the DEA as the optimal choice (35).

Fig. 15

(a) $\mathsf{F}$ as a function of $L$ when $n_1=1.11$, $n_2=2.40$, and $R/L=0.25$, (b) $\mathsf{F}$ as a function of $n_1$ and $n_2$ when $L=430\mathrm{nm}$ and $R/L=0.25$, and (c) $\mathsf{F}$ as a function of $R/L$ when the remaining parameters are fixed at their optimal values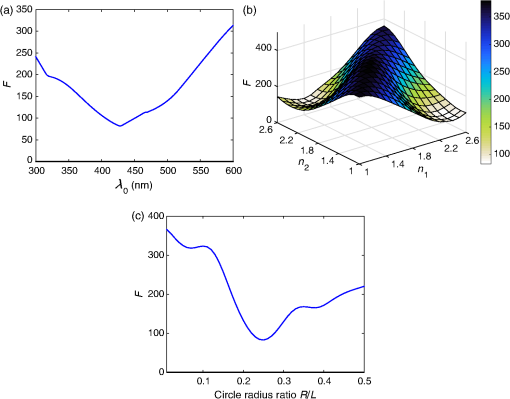: $L=440\text{nm}$, $n_1=1.11$, and $n_2=2.40$.

Next, we fixed $L=440\text{nm}$ and $R/L=0.25$ at their optimal values, and plotted $\mathsf{F}$ against $n_1$ and $n_2$ in Fig. 15(b). In this case, there are two local minima. One has $n_1<n_2$, the other $n_1>n_2$. Both minima give the same order of magnitude of $\mathsf{F}$, and DEA chooses $\{n_1=1.11,n_2=2.40\}$ correctly in Sec. 4.2.2. In Sec. 4.2.1, this choice was ruled out by the stringent constraint on $n_2$ in (31). The local minimum when $n_2<n_1$ (in Sec. 4.2.1) also gives a small value of $\mathsf{F}$.

Finally, we fixed the parameters $n_1=1.11$, $n_2=2.40$, and $L=430\mathrm{nm}$. Figure 15(c) presents $\mathsf{F}$ as a function of the ratio $R/L$. Clearly, $\mathsf{F}$ reaches the global minimum when $R/L=0.25$ as predicted by DEA. Besides the global minimum, the graph shows that $\mathsf{F}$ has two other local minima. These local minima could trap a gradient search algorithm¹⁶ and justify the use of the DEA or some other algorithm designed to avoid local minima.

5.

Concluding Remarks

We have demonstrated with two candidate devices that the combination of RCWA and DEA is a useful tool for designing gratings intended for splitting the solar spectrum. By adjusting a reasonable initial guess and defining a suitable search space, we can optimize the structural and constitutive parameters of candidate splitter designs. Greater optimization would require us to allow more changes in the design (e.g., perhaps shapes) but would require more computational time and might result in structures that are hard to manufacture. Experimental validation of a structure similar to the optimized splitter with circular grating elements is being pursued.